TAREAS DE ALGEBRA
ESTE BLOG SE CREO CON LA FINALIDAD DE RESOLVER TUS DUDAS EN LAS TAREAS, PARA QUE PUEDAS RESOLVERLAS SATISFACTORIAMENTE.
NADA MAS RECUERDA QUE DEBES ESTAR CONSTANTEMENTE EN COMUNICACIÓN
UNA VEZ VISTO ESTE VIDEO RESUELVE LAS SIGUIENTES ECUACIONES
LEER EL SIGUIENTE TEXTO PARA LA CLASE DEL JUEVES
Ecuación cuadrática
| Esto es una ecuación cuadrática: |
 |
| (a, b, y c pueden tener cualquier valor, excepto que a no puede ser 0.) |
La letra "x" es la variable o incógnita, y las letras a, b y c son los coeficientes (lee lasDefiniciones básicas de Álgebra)
|
Y el nombre cuadrática viene de "cuad" que quiere decir cuadrado, porque el exponente más grande es un cuadrado (en otras palabras x2).
|
Ejemplos de ecuaciones cuadráticas:
| En esta a=2, b=5 y c=3 | ||
Aquí hay una un poco más complicada:
| ||
| ¡Ups! Esta no es una ecuación cuadrática, porque le falta el x2 (es decir a=0, y por eso no puede ser cuadrática) |
¿Qué tienen de especial?
Las ecuaciones cuadráticas se pueden resolver usando una fórmula especial llamada fórmula cuadrática:
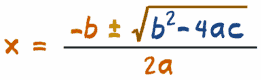
| El "±" quiere decir que tienes que hacer más Y menos, ¡así que normalmente hay dos soluciones! | |
La parte azul (b2 - 4ac) se llama discriminante, porque sirve para "discriminar" (decidir) entre los tipos posibles de respuesta:
|
Solución
Para resolverla, sólo pon los valores de a,b y c en la fórmula cuadrática y haz los cálculos.
Ejemplo: resuelve 5x² + 6x + 1 = 0
Fórmula cuadrática: x = [ -b ± √(b2-4ac) ] / 2a
Los coeficientes son: a = 5, b = 6, c = 1
Sustituye a,b,c: x = [ -6 ± √(62-4×5×1) ] / 2×5
Resuelve: x = [ -6 ± √(36-20) ]/10 = [ -6 ± √(16) ]/10 = ( -6 ± 4 )/10
Respuesta: x = -0.2 and -1
(Comprobación:
5×(-0.2)² + 6×(-0.2) + 1 = 5×(0.04) + 6×(-0.2) + 1 = 0.2 -1.2 + 1 = 0
5×(-1)² + 6×(-1) + 1 = 5×(1) + 6×(-1) + 1 = 5 - 6 + 1 = 0)
5×(-0.2)² + 6×(-0.2) + 1 = 5×(0.04) + 6×(-0.2) + 1 = 0.2 -1.2 + 1 = 0
5×(-1)² + 6×(-1) + 1 = 5×(1) + 6×(-1) + 1 = 5 - 6 + 1 = 0)
Ecuaciones cuadráticas disfrazadas
Algunas ecuaciones no parece que sean cuadráticas, pero con manipulaciones astutas se pueden transformar en una:
| Disfrazadas | Qué hacer | En forma estándar | a, b y c |
|---|---|---|---|
| x2 = 3x -1 | Mueve todos los términos a la izquierda | x2 - 3x + 1 = 0 | a=1, b=-3, c=1 |
| 2(x2 - 2x) = 5 | Desarrolla paréntesis | 2x2 - 4x - 5 = 0 | a=2, b=-4, c=-5 |
| x(x-1) = 3 | Desarrolla paréntesis | x2 - x - 3 = 0 | a=1, b=-1, c=-3 |
| 5 + 1/x - 1/x2 = 0 | Multiplica por x2 | 5x2 + x - 1 = 0 | a=5, b=1, c=-1 |
Hola compañera gracias por su blog espero que aportaciones me sirva par a repasar lo básico de matemáticas
ResponderBorrarSaludos
Hola Marichuy, si que va hacer de mucho apoyo este blog para los alumnos y porque no también para una servidora.
ResponderBorrarSaludos Caty
HOLA MARYCHUY!!!
ResponderBorrarMATEMATICASSSSS HEEEE!!
ME PONDRÉ A TRABAJAR
HOLA, AHORA SI PODEMOS COMPARTIR CONOCIMIENTOS
ResponderBorrarSALUDOS
GRACIAS... MARYCHUY, SABES ESTO ME SERA DE MUCHA UTILIDAD, POR QUE HACE AÑOSSSSSS, VI ESTO Y DEBO RECORDARLO PARA DUDAS DE MIS ALUMNOS Y MUY PRONTO MIS HIJITOS.
ResponderBorrarSALUDOS Y GRACIAS POR COMPARTIRLO.
NANCY